Interferenz: Stehende Welle
Stehende Welle als Sonderfall der Interferenz I
Bei den bisherigen Betrachtungen wurde noch nicht auf die Überlagerung der Wellen auf der Verbindungslinie zwischen den Erregern eingegangen. Auf dieser Geraden laufen Wellenberge und -täler aufeinander zu. Trifft ein Wellenberg des einen Erregers auf ein Wellental des anderen Erregers und besitzen diese gleiche Wellenlänge und Amplitude, addieren sich die Elongationen zu Null, wenn Berg und Tal genau aufeinander liegen. Da Wellen Energie transportieren, stellt sich zunächst die Frage, ob die Energie der Wellen durch die Addition der Elongationen zu Null – im Widerspruch zum Energieerhaltungssatz – verschwindet.
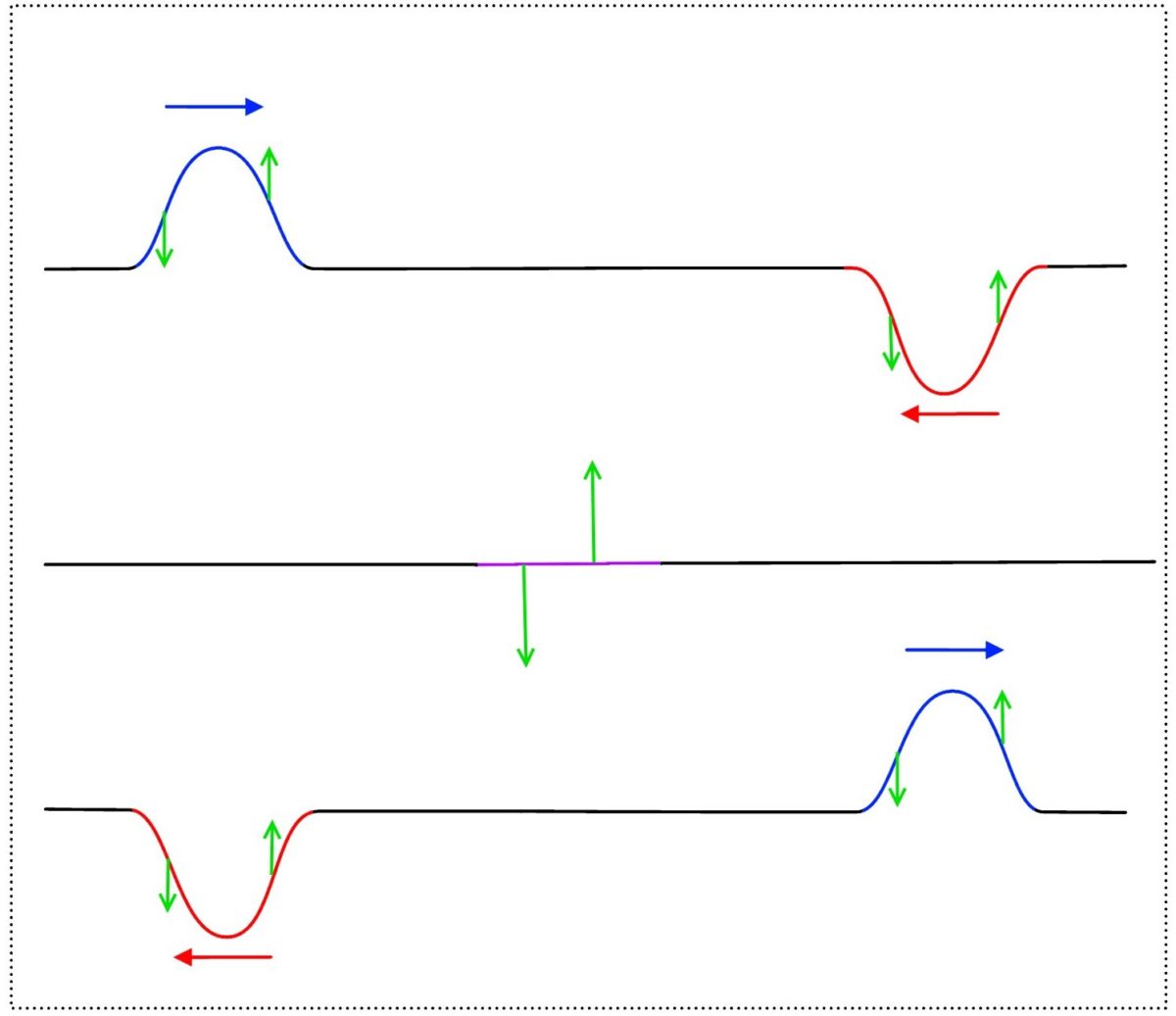
Die Energie der Wellenberge und -täler liegt nicht nur als Elongationsenergie der gekoppelten Teilchen vor, sondern auch als kinetische Energie. Überlagert sich wie im obigen Bild der nach rechts laufende Wellenberg exakt mit dem nach links laufenden Wellental, ist zwar für einen kurzen Augenblick keinerlei Elongationsenergie vorhanden, die Gesamtenergie liegt nun aber vollständig in Form von Bewegungsenergie der Teilchen vor. Zu erkennen ist dies an den oben grün eingezeichneten Pfeilen für die Teilchenschnellen. Zusammenfassend können wir formulieren:
Treffen zwei oder mehrere Störungen an einer Stelle eines Wellenträgers zusammen, so addieren sich dort deren Elongationen und Schnellen. Nach der Durchdringung laufen die Störungen unverändert weiter!
Die Simulation unten zeigt die Durchdringung der beiden aufeinander zulaufenden Störungen. Obwohl die Elongationen sich für einen kurzen Augenblick auslöschen, verschwinden Wellenberg und Wellental nicht, sondern sie durchlaufen sich, ohne ihr Aussehen zu verändern (in der Simulation treten durch das Simulationverfahren Quantisierungsfehler auf).
Stehende Welle als Sonderfall der Interferenz II
Im Bild unten ist der Fall zu sehen, bei dem zwei Wellenberge aufeinander zulaufen. Hier gibt es einen kurzen Augenblick, in dem keinerlei Bewegungsenergie vorhanden ist. Die Schnellen der beiden Wellenberge addieren sich dabei zu Null.
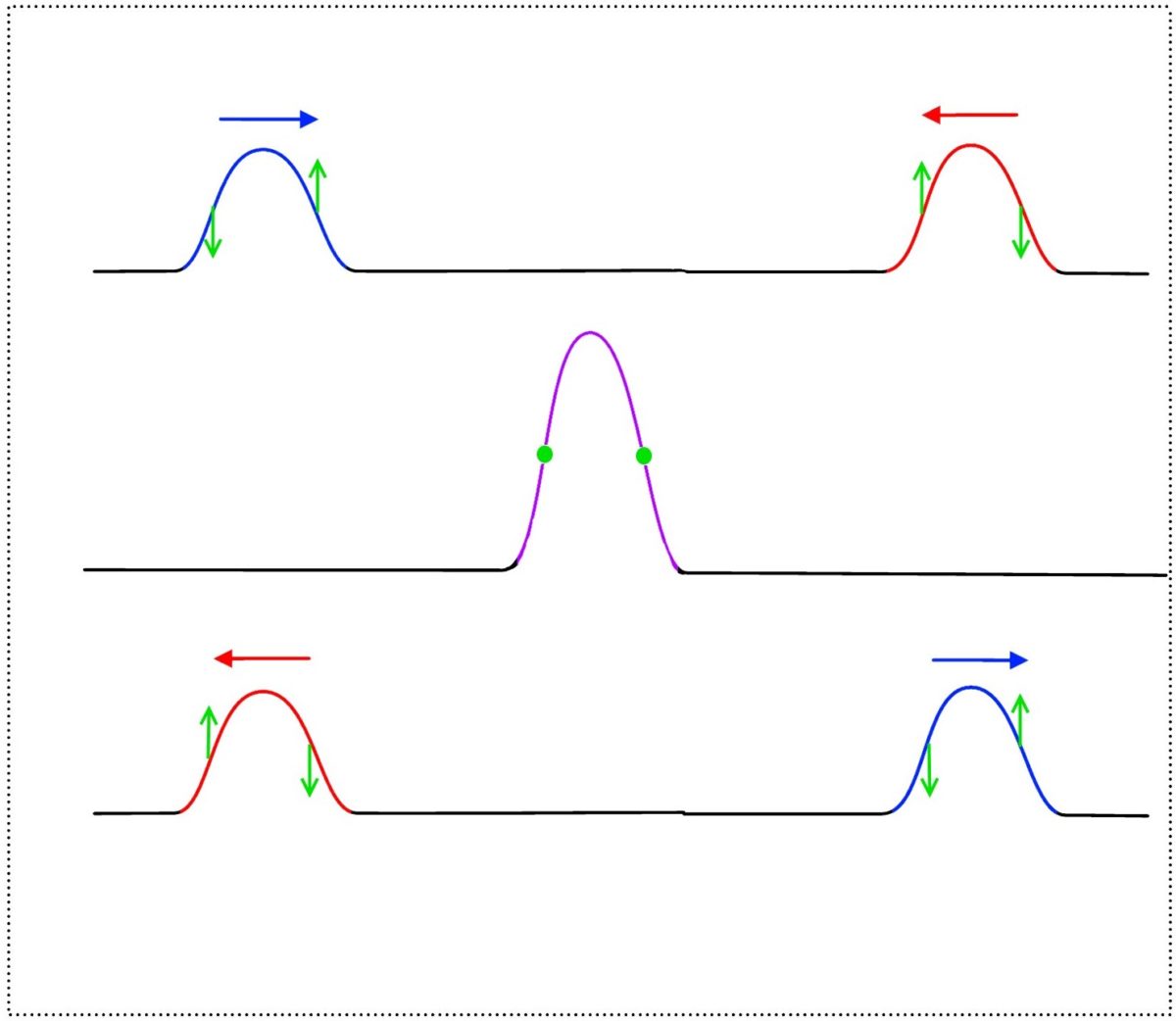
Die Simulation unten zeigt die Durchdringung der beiden aufeinander zulaufenden Wellenberge.
Die Störungen müssen nicht gleiche Amplitude oder Frequenz haben um sich ungestört zu durchlaufen. Die folgende Simulation zeigt das Durchlaufen eines großen Wellenberges und eines kleineren Wellentales.
Dieses ungestörte Durchdringen gilt nicht nur für mechanische Wellen, sondern auch für Radio- und Lichtwellen und ermöglicht es so, auf vielen unterschiedlichen Frequenzen Informationen von vielen Sendern zu vielen Empfängern zu transportieren. Im Gegensatz zu den mechanischen Wellen überlagern sich hier aber nicht Elongationen und Schnellen, sondern elektrische und magnetische Feldstärken.
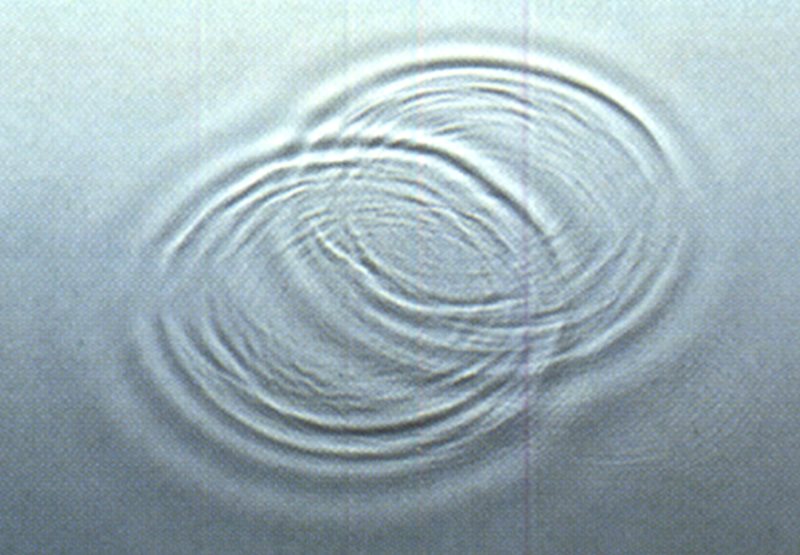
Das Bild unten zeigt noch einmal die Aufnahme der beiden kreisförmigen Wasserwellen von weiter vorne. Sehr schön ist zu sehen, dass die Störungen sich in ihrer Ausbreitung nicht gegenseitig beeinflussen.
Stehende Welle als Sonderfall der Interferenz III
Die Tatsache, dass sich die beiden von den Erregern ausgehenden Wellen ungehindert durchdringen, führt dazu, dass sich in der Verlängerung der Verbindungslinie der Erreger (dort wo Δs maximal ist), die Wellen nicht anders überlagern, als in der übrigen Schwingungsebene. Ein Auslöschen der Wellen findet also nicht statt, obwohl Wellenberge und -täler in der Verbindungsline der Erreger aufeinandertreffen. Dennoch lässt sich zwischen den Erregern eine Besonderheit feststellen, die in der folgenden Animation gut zu sehen ist.
Während links vom linken Erreger und rechts vom rechten Erreger ausgehend, sich im Raum fortschreitende Wellen beobachten lassen, findet man zwischen den Erregern keine sich transversal ausbreitende Welle. Dennoch ist Bewegung vorhanden. Eine solche, nicht fortschreitenden Welle, bezeichnet man als „Stehende Welle“. Wie sich eine stehende Welle (rot) aus den beiden gegenläufigen Wellen (blau und grün) bildet, wird in der Animation unten gezeigt.
Stehende Welle als Sonderfall der Interferenz IV
Voraussetzung für die Bildung einer stehenden Welle sind gleiche Amplitude und Frequenz. In der Animation unten ist beispielsweise die Amplitude der nach links laufenden Welle (grün) etwas kleiner, als die der nach rechts laufenden (blau). Aus diesem Grund kommt es zu einem regelmäßigen Rucken der Gesamtwelle (rot) nach rechts.
Stehende Welle als Sonderfall der Interferenz V
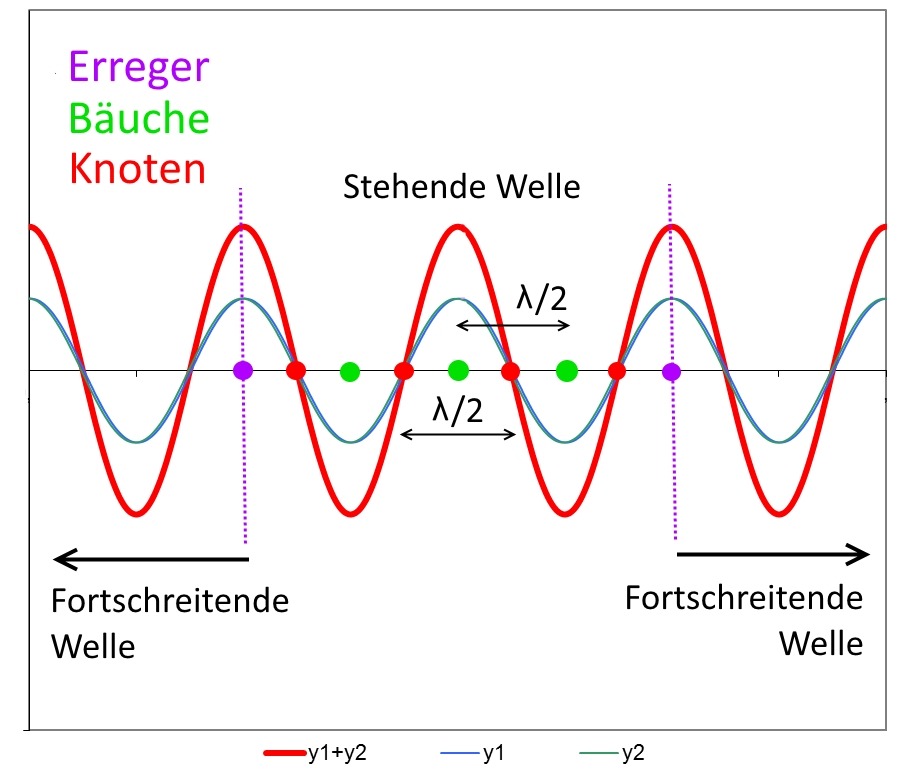
In der Animation unten ist auf der Verbindungslinie zwischen (-2|-5) und (+2|-5) eine stehende Welle zu beobachten. Bei den Erregern, aber auch an den Stellen zwischen den Erregern, an denen sich Maxima befinden, schwingen die Teilchen mit maximaler Amplitude. Diese Orte werden „Schwingungsbäuche” oder kürzer „Bäuche” genannt. Dazwischen finden sich Teilchen, die sich überhaupt nicht bewegen. Sie bilden sogenannte „Schwingungsknoten” oder „Knoten”.
Im Bild unten erkennt man, dass an den Stellen, wo sich die Maxima-Linien mit der Verbindungslinie der Erreger schneiden, Bäuche auftreten. Die Knoten findet man an den Schnittpunkten mit den Minima-Linien.
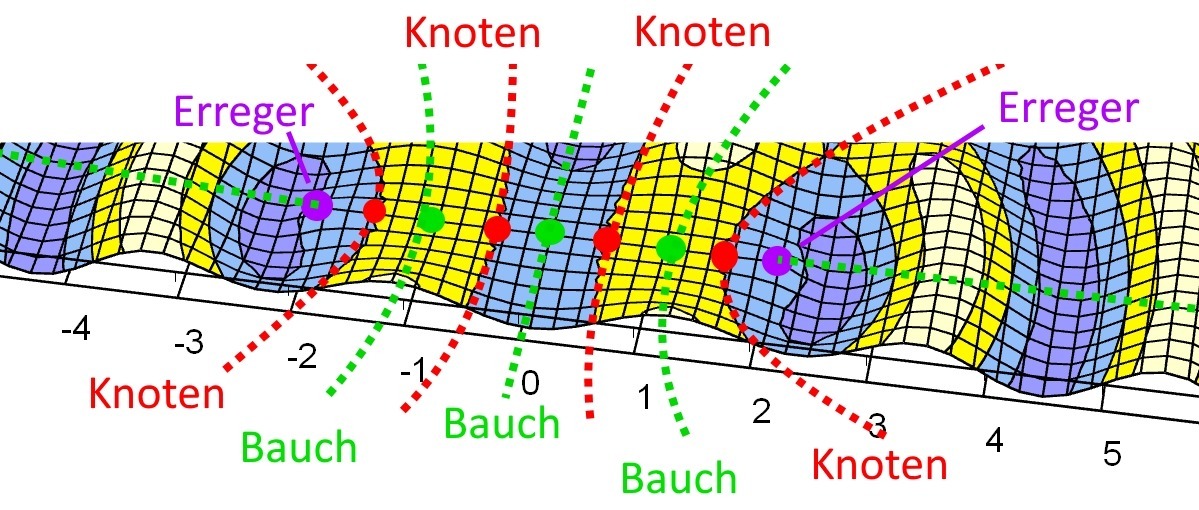
Im Bild unten ist ein Schnitt durch die Erregerverbindungslinie zu sehen. Knoten und Bäuche haben als Abstand eine halbe Wellenlänge.
Alle Materialien auf der Webseite vibos.de, die auch als solche gekennzeichnet sind, stehen als OER – Open Educational Resources zur freien Verfügung und unter Creative Commons-Lizenz. Sie dürfen unter Angabe der Herkunft [CC BY SA 4.0 VIBOS – Virtuelle Berufsoberschule Bayern] weiterverwendet und verlinkt werden.



