Überblick zu den Inhalten in diesem Kapitel
Nachdem wir nun wissen, wie man Geraden in einem 3-dimensionalen Koordinatensystem mithilfe von vektoriellen Gleichungen beschreiben kann, wenden wir uns Situationen zu, in denen sich gleich 2 (oder mehr) Geraden gleichzeitig in dem selben 3-dimensionalen Koordinatensystem befinden.
Die vektoriellen Geradengleichungen helfen uns dabei herauszufinden, welche Lage eine Gerade bzgl. einer anderen Geraden hat.
Dieses Kapitel handelt von
- von der Untersuchung der Lagebeziehungen zweier Geraden und
- von der Ermittlung der Schnittmenge beider Geraden, die eine wichtige Rolle bei der Untersuchung der Lagebeziehung spielt.
Mögliche Lagebeziehungen zweier Geraden
Zwei Geraden können im 3-Dimensionalen folgende Lagebeziehungen haben:
g und h sind identisch
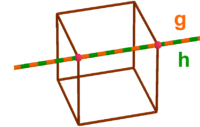
g und h sind echt parallel
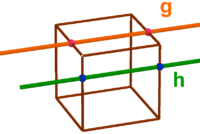
g und h schneiden sich in genau einem Punkt
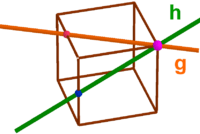
g und h sind windschief
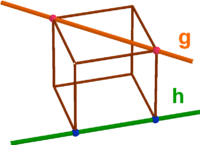
Aufgabe
a) Beschreiben Sie für jede der 4 möglichen Lagebeziehungen die jeweilige Schnittmenge.
b) Entscheiden Sie, ob mit der Angabe der Schnittmenge die jeweilige Lagebeziehung der beiden Geraden eindeutig beschrieben wird.
Interaktive Untersuchung der Lagebeziehung zweier Geraden
Verändern Sie die Lage der beiden Geraden in dem folgenden Geogebra-Applet, indem Sie die Punkte A, B, P und Q mithilfe der Maus verschieben.
Das Applet zeigt Ihnen sofort mögliche Geradengleichungen an. Ebenso werden die Lagebeziehung und gegebenenfalls die Koordinaten eines Schnittpunkts angegeben.
Versuchen Sie, die 4 verschiedenen Lagebeziehungen zu erzeugen:
- identisch
- echt parallel
- in einem Punkt schneidend
- windschief
Beobachten Sie dabei die zugehörigen Geradengleichungen. Betrachten Sie dabei die Richtungsvektoren in den Geradengleichungen und versuchen Sie zu erkennen, ob die Richtungsvektoren linear abhängig sind.
Die Punkte sind zwecks einfacherer Positionierung an verschiedene Seitenflächen des Hilfsquaders gebunden, aber Sie können diese Bindung auch ausschalten.
Fragen
Versuchen Sie, folgende Fragen zu beantworten:
1) Wenn sich 2 Geraden im 3-dimensionalen Raum nicht schneiden, welche Lagebeziehung können sie dann haben?
2) Wenn die Richtungsvektoren von 2 Geraden im 3-dimensionalen Raum linear abhängig sind, welche Lagebeziehung können die beiden Geraden dann haben?
Erste Überlegungen für die Vorgehensweise zur Untersuchung der Lagebeziehung
Um die Lagebeziehung der beiden Geraden zu bestimmen, werden wir die Schnittmenge der beiden Geraden ermitteln (und zwar mithilfe eines geeigneten Gleichungssystems) und die Verwandtschaft der beiden Richtungsvektoren untersuchen:
- Um herauszufinden, ob beide Geraden keinen, einen oder unendlich viele Punkte gemeinsam haben, verwendet man ebenfalls die zugehörigen vektoriellen Geradengleichungen, was uns schließlich zu einem linearen Gleichungssystem mit 3 Gleichungen und 2 Variablen führt.
- An den Richtungsvektoren erkennt man sehr schnell, ob die beiden Geraden parallel sind oder nicht.
Vorgehensweisen zur Ermittlung der Lagebeziehung zweier Geraden
Die Antwort zur folgenden Frage erläutert die Vorgehensweise zur Ermittlung der Schnittmenge zweier Geraden.
Wie kann man mithilfe eines Gleichungssystems vorgehen, um die Lagebeziehung zweier Geraden zu ermitteln?
Erinnerung: Lösen von Gleichungssystemen
Da für die Ermittlung der Schnittmenge zweier Geraden die Fähigkeit, Gleichungssysteme effizient lösen zu können, von entscheidender Bedeutung ist, können Sie hier noch einmal Ihre Kenntnisse dazu auffrischen.
Schrittweise Vorgehensweise für die Untersuchung der Lagebeziehung
In dem folgenden Geogebra-Applet wird für zufällige Situationen vorgeführt, wie man vorgehen kann, um die Lagebeziehung zweier Geraden zu ermitteln. Dabei wird jeweils
- die Schnittmenge beider Geraden mithilfe eines geeigneten Gleichungssystems ermittelt und
- anschließend evtl. noch die lineare Abhängigkeit der Richtungsvektoren beider Geraden untersucht.
WICHTIG:
Verfolgen Sie die Lösungen für verschiedene Situationen (dazu auf die Neu-Schaltfläche klicken), und zwar so oft, bis Sie alle möglichen Fälle (identisch, echt parallel, in einem Punkt schneidend, windschief) nachvollziehen konnten.
Anleitung:
- Zu jeder Situation können Sie sich einen Lösungsweg Schritt für Schritt vorführen lassen. Klicken Sie dazu auf die Schaltfläche mit dem Pfeil nach rechts. . Falls Sie die Aufgabe selber lösen wollen, überlegen Sie vor jedem weiteren Schritt, ob Sie nicht doch vielleicht ohne weitere Tipps auskommen.
- Falls die Aufgabenstellung oder die Lösung nicht vollständig angezeigt wird (insbesondere, wenn Sie das Gefühl haben, dass am Ende der Lösung eine Folgerung fehlt), können Sie die Trennlinie zwischen dem Aufgaben- und dem Lösungsbereich und der 3D-Graphik mithilfe der Maus verschieben
- Falls Sie die 3D-Graphik dazuschalten, müssen Sie im 3D-Fenster evtl. zoomen, um die Geraden zu sehen.
Alle Materialien auf der Webseite vibos.de, die auch als solche gekennzeichnet sind, stehen als OER – Open Educational Resources zur freien Verfügung und unter Creative Commons-Lizenz. Sie dürfen unter Angabe der Herkunft [CC BY SA 4.0 VIBOS – Virtuelle Berufsoberschule Bayern] weiterverwendet und verlinkt werden.



